前回の続き。only if を示します。
Categorical Logic and Type Theory, Volume 141 (Studies in Logic and the Foundations of Mathematics)
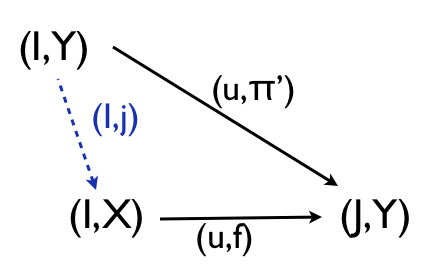
まず、(u,f)がカルテシアンなので、(u,π'):(I,Y)→(J,Y)とIに関して、以下を可換にするようなj:I×Y→Xが存在します。
このjに対して、h^-1 = <π,j> と定義します。<π,j>は以下の図のようになります。この図は上の可換性を元の圏の射で表したものであり、これによってh^-1が求める射が満たすべき可換性を満たすことがわかります。
後は、このh^-1がisoになるかどうか。ここで h = <π,f>と定義すると、h;h^-1 = I×X かつ h^-1;h = I×Y となります。
まず、h^-1;h = I×Yは、以下の図で <π,π'> = I×Y、 <π,π'> = <π,j>;<π,f> であり、直積の一意性から言えます。
最後、h;h^-1 = I×Xですが、まずは以下の図を考えます。(u,f)とIについて、緑の射も青の射も図を可換にします*1が、(u,f)がカルテシアンなのでこの射は一意となります。つまり、(I,f);(I,j) = (I,π')です。
この等式を元の圏で考えると、以下の図になります。ここで、<π,π'> = I×X = <π,f>;<π,j> なので、h;h^-1 = I×Xが言えます。
*1:上の三角形が可換かは確かめる必要がありますが、定義通り計算すれば自明です。